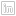PostGIS Polygon Splitting

One of the joys of geospatial processing is the variety of tools in the tool box, and the ways that putting them together can yield surprising results. I have been in the guts of PostGIS for so long that I tend to think in terms of primitives: either there’s a function that does what you want or there isn’t. I’m too quick to ignore the power of combining the parts that we already have.

A community member on the users list asked (paraphrased): “is there a way to split a polygon into sub-polygons of more-or-less equal areas?”

I didn’t see the question, which is lucky, because I would have said: “No, you’re SOL, we don’t have a good way to solve that problem.” (An exact algorithm showed up in the Twitter thread about this solution, and maybe I should implement that.)

PostGIS developer Darafei Praliaskouski did answer, and provided a working solution that is absolutely brilliant in combining the parts of the PostGIS toolkit to solve a pretty tricky problem. He said:

The way I see it, for any kind of polygon:

• Convert a polygon to a set of points proportional to the area by ST_GeneratePoints (the more points, the more beautiful it will be, guess 1000 is ok);
• Decide how many parts you’d like to split into, (ST_Area(geom)/max_area), let it be K;
• Take KMeans of the point cloud with K clusters;
• For each cluster, take a ST_Centroid(ST_Collect(point));
• Feed these centroids into ST_VoronoiPolygons, that will get you a mask for each part of polygon;
• ST_Intersection of original polygon and each cell of Voronoi polygons will get you a good split of your polygon into K parts.

Let’s take it one step at a time to see how it works.

We’ll use Peru as the example polygon, it’s got a nice concavity to it which makes it a little trickier than an average shape.

CREATE TABLE peru AS 
  SELECT *
  FROM countries
  WHERE name = 'Peru'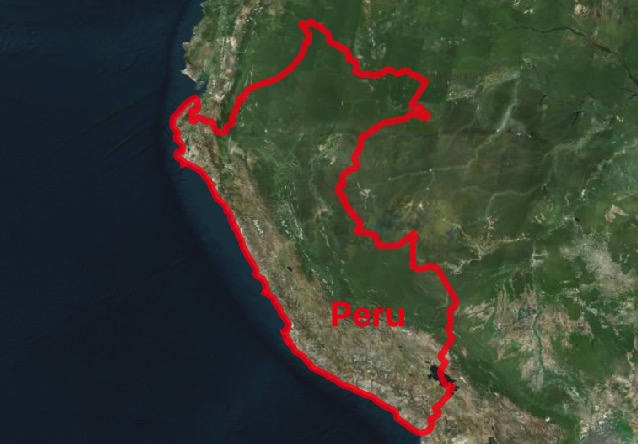

Now create a point field that fills the polygon. On average, each randomly placed point ends up “occupying” an equal area within the polygon.

CREATE TABLE peru_pts AS
  SELECT (ST_Dump(ST_GeneratePoints(geom, 2000))).geom AS geom
  FROM peru
  WHERE name = 'Peru'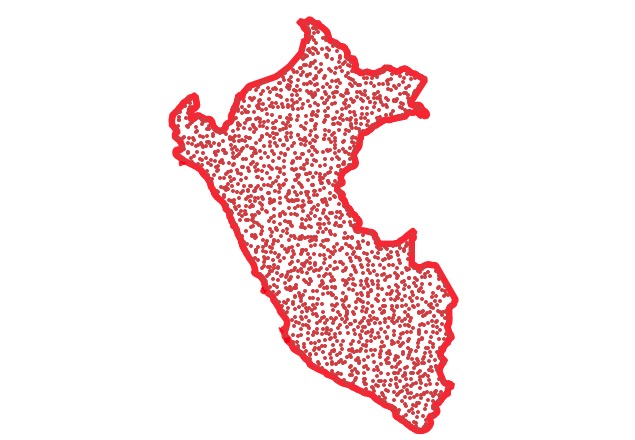

Now, cluster the point field, setting the number of clusters to the number of pieces you want the polygon divided into. Visually, you can now see the divisions in the polygon! But, we still need to get actual lines to represent those divisions.

CREATE TABLE peru_pts_clustered AS
  SELECT geom, ST_ClusterKMeans(geom, 10) over () AS cluster
  FROM peru_pts;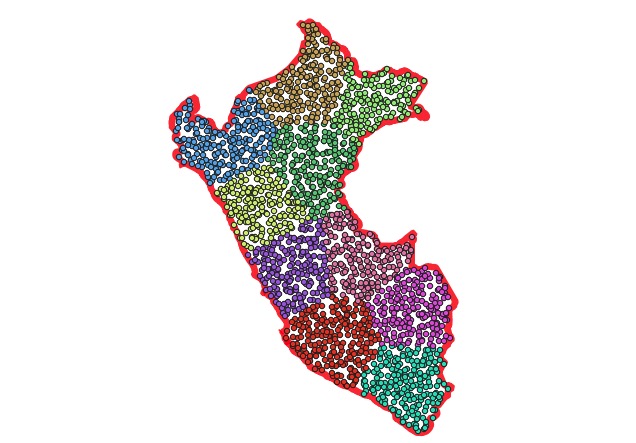

Using a point field and K-means clustering to get the split areas was inspired enough. The steps to get actual polygons are equally inspired.

First, calculate the centroid of each point cluster, which will be the center of mass for each cluster.

CREATE TABLE peru_centers AS
  SELECT cluster, ST_Centroid(ST_collect(geom)) AS geom
  FROM peru_pts_clustered
  GROUP BY cluster;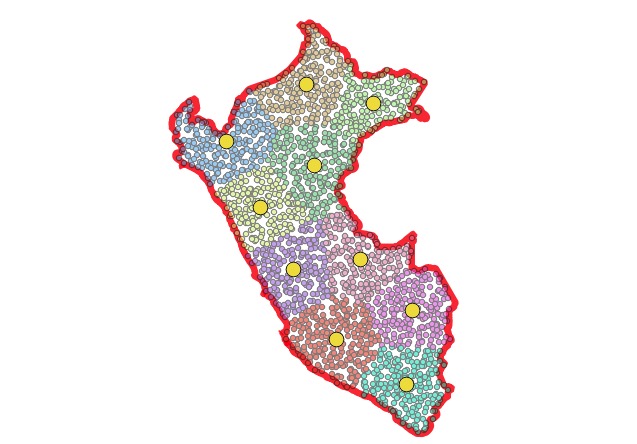

Now, use a voronoi diagram to get actual dividing edges between the cluster centroids, which end up closely matching the places where the clusters divide!

CREATE TABLE peru_voronoi AS
  SELECT (ST_Dump(ST_VoronoiPolygons(ST_collect(geom)))).geom AS geom
  FROM peru_centers;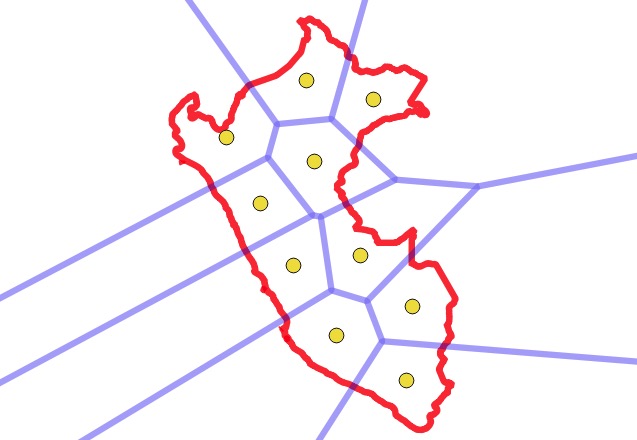

Finally, intersect the voronoi areas with the original polygon to get final output polygons that incorporate both the outer edges of the polgyon and the voronoi dividing lines.

CREATE TABLE peru_divided AS
  SELECT ST_Intersection(a.geom, b.geom) AS geom
  FROM peru a
  CROSS JOIN peru_voronoi b;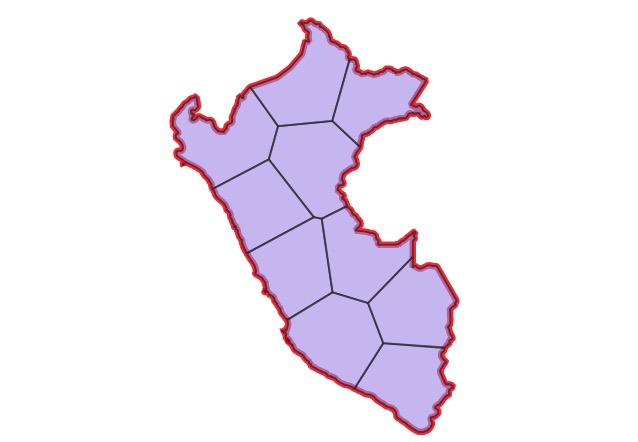

Done!

Clustering a point field to get mostly equal areas, and then using the voronoi to extract actual dividing lines are wonderful insights into spatial processing. The final picture of all the components of the calculation is also beautiful.

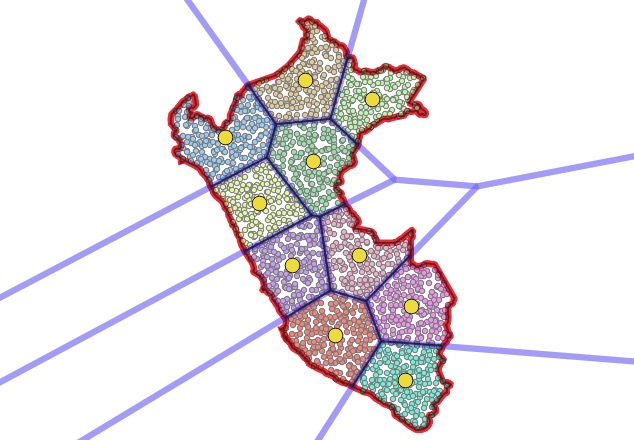
I’m not 100% sure, but it might be possible to use Darafei’s technique for even more interesting subdivisions, like “map of the USA subdivided into areas of equal GDP”, or “map of New York subdivided into areas of equal population” by generating the initial point field using an economic or demographic weighting.